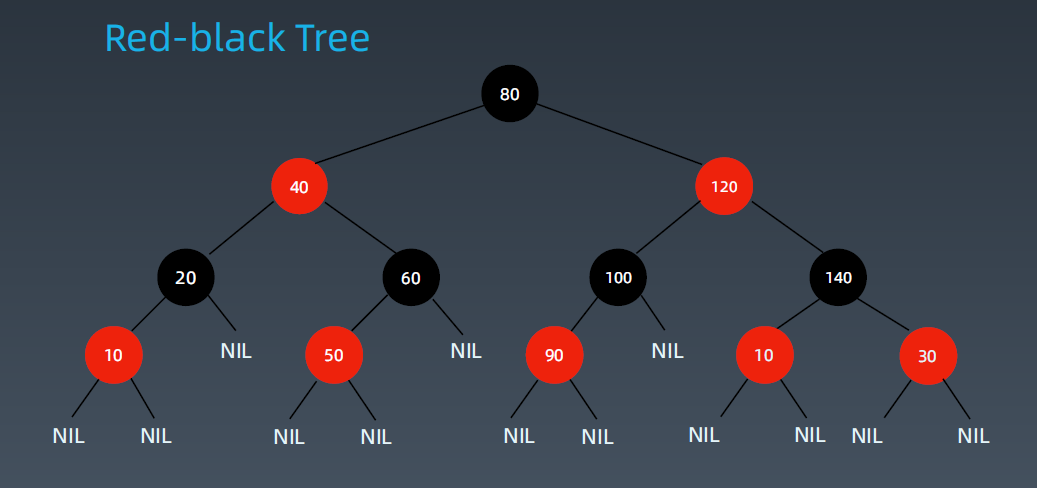
红黑树(Red Black Tree)是一种自平衡二叉查找树。

所谓自平衡，就像高中生物中学过的“去除顶端优势”，通过去除植物顶端优势，侧芽会迅速生长变得强壮，整棵植物变得平衡。红黑树也是同理，利用旋转去除顶端优势，使二叉树达到相对平衡。

红黑树的每个节点都遵循以下规则：

（1）每个节点都有颜色，黑色或红色。

（2）根节点是黑色的。

（3）每个叶子节点（NIL）是黑色的。（这里的叶子节点指的是为空(NIL或NULL)的叶子节点！]

（4）红色节点的子节点必定是黑色的。（没有连续的红节点）

（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。（红黑树保证最长路径不超过最短路径的二倍，因而近似平衡。）

红黑树有两大操作:

  1. recolor (重新标记黑色或红色)
  2. rotation (旋转，这是树达到平衡的关键)

添加节点

每次插入新节点X时：

  1. 将新插入的节点标记为红色
  2. 如果 X 是根结点(root)，则标记为黑色
  3. 如果 X 的 father 是红色：
  • 3.1 如果 X 的 uncle 是红色
    • 3.1.1 将 father 和 uncle 标记为黑色
    • 3.1.2 将 grandfather 标记为红色
    • 3.1.3 把 grandfather 当成新插入节点重复步骤 2、3
  • 3.2 如果 X 的 uncle 是黑色，我们要分四种情况处理：（ f:father ; g:grandfather ; u:uncle ; b:brother ; l:leftchild ; r:rightchild）
    • 3.2.1 左左 (f 是 g 的左孩子，并且 X 是 f 的左孩子)
    • 3.2.2 左右 (f 是 g 的左孩子，并且 X 是 f 的右孩子)
    • 3.2.3 右右 (和 左左 镜像过来，恰好相反)
    • 3.2.4 右左 (和 左右 镜像过来，恰好相反)

左左：把 f 点提起来，g 点放下去；b 点成为 g 节点的子节点；改变 f 点和 g 点颜色；f 点成为 g 点父节点的子节点；同时把 f 点当成新的插入点。

redBlackTreeLeftLeft

右右：把 f 点提起来，g 点放下去；b 点成为 g 节点的子节点；改变 f 点和 g 点颜色；f 点成为 g 点父节点的子节点；同时把 f 点当成新的插入点。

redBlackTreeRightRight

左右：把 X 点提起来，f 点放下去；l 点成为 f 点子节点；X 点成为 g 点子节点；把 f 点当成新插入点运用左左情况解决。

redBlackTreeLeftRight

右左：把 X 点提起来，f 点放下去；r 点成为 f 点子节点；X 点成为 g 点子节点；把 f 点当成新插入点运用右右情况解决。

redBlackTreeRightLeft

删除节点

将红黑树内的某一个节点删除，需要执行的操作依次是：首先，将红黑树当作一颗二叉查找树，将该节点从二叉查找树中删除；然后，通过rotation和recolo来修正该树，使之重新成为一棵红黑树。

二叉查找树删除节点根据节点位置会有以下三种情况：

  • 删除节点的度为0，则直接删除
  • 删除节点的度为1，则该子节点替代删除节点
  • 删除节点的度为2，则从左子树中寻找值最大的节点替代删除节点。对树结构改动最少、最适合替代删除节点的必然是左子树中的最大叶子节点与右子树中的最小叶子节点

红黑树和二叉查找树的删除类似，只不过加上颜色属性（这里的子节点均指非NULL节点）：

  • 无子节点时，删除节点可能为红色或者黑色；
    1.1 如果为红色，直接删除即可，不会影响黑色节点的数量；
    1.2 如果为黑色，则需要进行删除平衡的操作了；
  • 只有一个子节点时，删除节点只会是黑色，其子节点为红色，否则无法满足红黑树的性质。 此时用删除节点的子节点接到父节点，且将子节点颜色涂黑，保证黑色数量。
  • 有两个子节点时，与二叉搜索树一样，使用后继节点（一般是左子树的最大叶子节点）作为替换的删除节点，情形转至为1或2处理。

我们发现，删除情形3总是会转换为情形1和2的，而情形1.1和情形2处理平衡非常简单，本文主要讨论的是情形1.2：删除黑色的叶子节点。因为一旦该节点被拿掉，红黑树中通过该节点的路径黑色节点数量将会减1，而且无法像情形2那样将子节点涂黑来达到平衡。此时只能自底向上进行平衡操作。

redBlackTreeExample

redBlackTreeSort

一个在线的红黑树演示工具：https://www.cs.usfca.edu/~galles/visualization/RedBlack.html